Understanding How Process Behaviour Charts Work
Demystifying the Swiss Army Knife of Data Analysis
THE AIM of this post is to re-publish a LinkedIn article I wrote in August of 2020 on the topic of how Process Behaviour Charts work from theory to application. I’ve previously written about PBCs in this newsletter on Nov. 5/21 (Control Charts), and Feb. 3/22 (A Rational Basis for Prediction), however I wanted to bring this post out to subscribers here who might find it useful to answer questions that naturally arise from learning about this form of process data analysis, questions that I had when I was studying them for the first time. Let me know your thoughts in the comments below.
NB: In reading over the article I can see I left out an important detail from Dr. Wheeler about whether the data you’re analyzing needs to be “normalized” or follow a particular distribution. The methods he describes for calculating the limits can be applied to any data set regardless of distribution.
NB 2: If you want to play around with process behaviour charts using different data sets, check out the free version of my web app, PBC Analyzer PRO. You can use it to quickly analyze the included data series for signals, shifting limits to segment the data into new periods like an old pro.
BONUS FOR SUBSCRIBERS: Get a copy of my Excel PBC template I use to quickly generate charts from time series data! All you need to do is paste in your own data and adjust the avg and mr-bar formulas to match the period you want to analyze. I’ll be running through some of my charts and how I use the template in a future post.
The aim of this short article is to take a shallow dive into the theory and clockworks behind Process Behaviour Charts so as to demystify how they work and to aid in creating and interpreting them more effectively. Specifically, I will be covering three topics in this regard:
The Empirical Rule
Calculating limits using sigma estimates vs. standard deviation calculations
Degrees of Freedom in data used to calculate estimates, and how much is needed to create useful limits.
Why Process Behaviour Charts?
It's worth recalling that the reason we want to visualize process data on a Process Behaviour Chart (PBC) is to avoid over or under reacting to patterns of variation. Without the guidelines that PBCs provide, through three sigma limits, it's impossible to confidently separate exceptional variation in the data from the random, routine noise.
While many people can use a PBC without understanding how it works by just looking for patterns of exceptional variation, your use of the charts (and by extension, skepticism of auto-generated ones) is enhanced when you understand some theory.
Let's begin:
Empirical Rule
The aim of a process behaviour chart is to quickly validate the homogeneity or statistical similarity of a stream of data. Three sigma limits are calculated and applied to provide the user with an easy way to separate signals from random noise. However, it's often asked why three sigma limits are chosen.
The underlying theory that supports this is called the Empirical Rule, which states that given a homogenous set of data:
Roughly 60%-75% of the data will be located within one sigma unit around the average.
Usually 90%-98% of the data will be located within two sigma units around the average.
Approximately 99%-100% of the data will be located within three sigma units around the average.[1]
A sigma unit converts the measurement units on a run chart to a convenient "scale" which tells us how much data dispersion we can estimate to fall on either side of the average. As the Empirical Rule suggests, we can envision each strata of sigma units as progressively finer filters that allow fewer data points to "fall through". Those that escape the three sigma limits are said to be exceptional, while those within are said to be routine. The gap between these limits is known as the voice of the process.
Below is a run chart of seventy-three data points describing a system of queues of test specimens that are either awaiting analysis or are in-process. The red dots signify data reported for Sundays. Those data that fall within one sigma of the average are highlighted in a rose-colored box: Forty-one data points escape the one sigma limits.
EDIT: I’ve since lost the original chart, however, I think the limits were calculated against the first thirty data points.
Same run-chart, but now with a blue overlay showing the data that falls within two sigma of the average: Eighteen data points escape the two limits.
Finally, the same run-chart featuring a lighter blue overlay showing the data within three sigma of the average. Now only four data points escape the three sigma limits, providing potential signals of exceptional variation in the data:
By eliminating most of the data (94% in this instance), we now have four places to begin inquiry about what happened in the specimen backlog queues, and consequently a means to observe future improvements against.
Sigma vs Standard Deviation
A subsequent question that commonly arises when computing limits on a Process Behaviour Chart is whether the sigma unit is equivalent to a standard deviation and thus interchangeable. They are not, for two key reasons:
A standard deviation statistic is global in scope, presuming the data set is homogenous;
PBCs, which rely on sigma estimates that are applied to the average moving range (mR-BAR) of the data, test whether this assumption is true. [2]
It's worth recalling here that a PBC is predicated upon calculating the moving range of the data, which compares successive pairs of data points (mR). This key distinction localizes the variation across this cascading chain of pairs, which makes the use of standard deviation inappropriate to estimate the limits.
To illustrate, consider this snippet of the first ten rows of data used to create the above charts. Note the formula to calculate Backlog mR is the whole, absolute difference between the current and preceding row (ABS(n - (n-1))), while mR-BAR is the average of the first thirty mR data points:
As a consequence, the limits that are computed using three sigma estimates tend to be wider than those using a standard deviation, and thus are designed to reveal only exceptional variation in the underlying process data. In other words, three sigma limits help to avoid finding false signals.
Degrees of Freedom in the Limits
Another common question among new practitioners is how many data points are required to compute usable limits. Dr. Donald Wheeler notes that as few as four are sufficient, re-calculating as new data points are acquired. But, when do you stop? Theoretically, if we kept going, ultimately all data points would begin to fall within limits and their efficiency would be diminished. This is where it becomes useful to understand the notion of "Degrees of Freedom".
In his book, Twenty Things You Need to Know, Wheeler explains Degrees of Freedom as the inverse relationship between uncertainty in the three sigma estimates and the number of data points we use to compute them. [3] He expresses this with the formula:
Uncertainty in Limits = 1 / SQRT (2 * Degrees of Freedom [data points] )
This can be visualized using a simple plot:
Note how limits dramatically improve as up to ten data points are used, with returns beginning to diminish beyond thirty data points. Does this mean you always need thirty data points for a reliable PBC? No; use what is rational for your application and follow the patterns of variation. Get started with the data you have on-hand and re-calculate the limits as you go until either it becomes pointless or the limits signal a move in another direction.
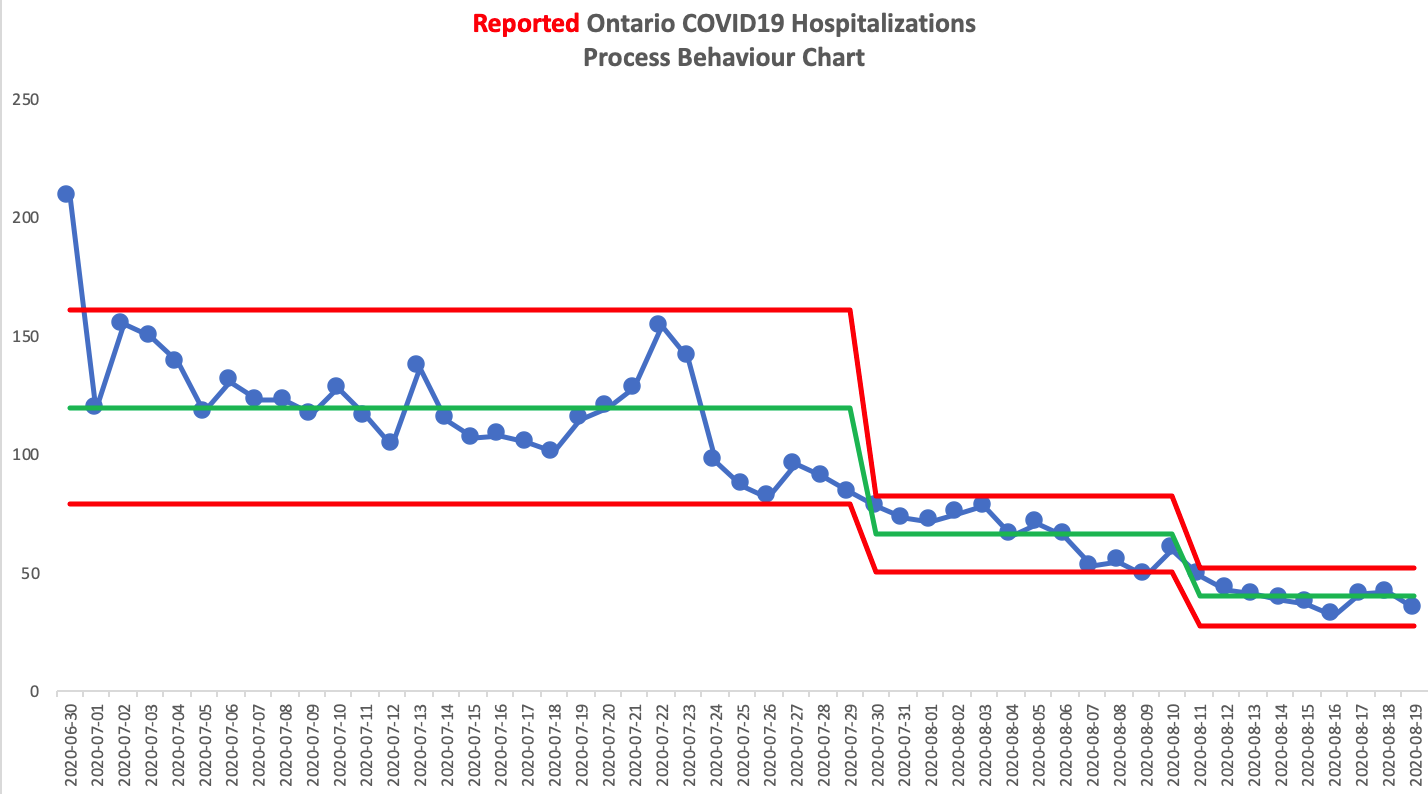
For example, when I am working with a pre-existing data set, I often begin my limit calculations using the first five to ten data points, incrementally adding more while looking for patterns that suggest I need to shift or re-calculate the limits in order to "follow the data". The plot below shows an example where successive limit calculations were required:
EDIT: Wheeler also advises that when it comes to deciding on whether to shift the limits it depends on the story you’re wanting to tell with the data. It’s not always required to do so. In this case, I wanted to show how the nature of variation in the data was changing over time.
Summary
The aim for this post was to demystify some of the theory behind Process Behaviour Charts: The Empirical Rule explains why three sigma limits are computed; sigma estimates are used instead of standard deviation because the homogeneity of the data is being tested and cannot be presumed; and finally, uncertainty in the limits improves as more data points are added, but diminishes beyond thirty.
Armed with this knowledge, you should now be able to create and critique PBCs more effectively and appreciate the decisions required to gain insights into how a process works by "hearing" its voice in the three sigma limits.
[1] Donald Wheeler, David Chambers. Understanding Statistical Process Control 2nd Ed., SPC Press, 1992, p. 61.
[2] Donald Wheeler. Twenty Things You Kneed to Know, SPC Press, 2009, p. 27.
[3] Ibid., pp. 60-61.