A Rational Basis for Prediction
Statistical Theory of Probability Doesn't Apply in the Experiences of Life
Rational prediction requires theory and builds knowledge through systematic revision and extension of theory based on comparison of prediction with observation.
Deming, W. Edwards. The New Economics, 3rd ed. (MIT Press) (p. 69). The MIT Press.
Sampling by use of random numbers. If we were to form lots by use of random numbers, then the cumulated average, the statistical limit of , would be 10. The reason is that the random numbers pay no attention to color, nor to size, nor to any other physical characteristic of beads, paddle, or employee. Statistical theory (theory of probability) as taught in the books for the theory of sampling and theory of distributions applies in the use of random numbers, but not in experiences of life. Once statistical control is established, then a distribution exists, and is predictable.
Deming, W. Edwards. Out of the Crisis (MIT Press) (p. 353). The MIT Press. Kindle Edition.
Prediction of variation. If we agree that the process showed statistical control good enough for use, we may extend the control limits into the future as prediction of the limits of variation of continued production. We have not in hand an additional four days, but we have data from the past to put on to the chart—same beads, same paddle, same foreman, different workers. We repeat here an important lesson about statistical control. A process that is in statistical control, stable, furnishes a rational basis for prediction for the results of tomorrow’s run.
Deming, W. Edwards. Out of the Crisis (MIT Press) (p. 350). The MIT Press. Kindle Edition.
Every observation, numerical or otherwise, is subject to variation. Moreover, there is useful information in variation. The closest approach possible to a numerical evaluation of any so-called physical content, to any count, or to any characteristics of a process is a result that emanates from a system of measurement that shows evidence that it is in statistical control.
Incidentally, the risk of being wrong in a prediction can not be stated in terms of probability, contrary to some textbooks and teaching. Empirical evidence is never complete.
Deming, W. Edwards. Out of the Crisis (MIT Press) (pp. 350-351). The MIT Press. Kindle Edition.
Dr. Shewhart was well aware that the statistician’s levels of significance furnish no measure of belief in a prediction. Probability has use; tests of significance do not.
Foreword to Shewhart, Walter A.. Statistical Method from the Viewpoint of Quality Control (Dover Books on Mathematics) . Dover Publications. Kindle Edition.
THE AIM for today's post is to gain a better understanding of what Dr. Deming called a rational basis for prediction. To do this, we're going to revisit his Red Bead Experiment, in particular the debriefing he would conduct afterward to probe and reveal how misapplied statistical theory can cause us to fall into traps and make grievous errors of prediction. In the mix and for the bargain, I'll also share a bit of code I wrote in Python to test Deming's hypothesis about random sampling and cumulative averages and take a brief look at an example concerning forecasting a software delivery project.
The Debrief of the Red Beads
Let's begin with reviewing the main components of the Red Bead Experiment system. For those unfamiliar with the experiment, I did a brief overview you can read here.
One box or bucket;
4,000 small beads: 3,200 white (80%), 800 red (20%)
One standard issue paddle with 50 indentations in a 5 x 10 configuration
Standard Operating Procedure requires six participants, "Willing Workers", to use the paddle to draw out 24 sample lots of 50 beads with the aim to produce the fewest red beads per lot. Results from two experiments Dr. Deming conducted at his seminars are shown below:
In his debriefing, Dr. Deming would ask participants to make a prediction of what the overall cumulative average would “settle” toward, given the knowledge of the beads, paddle and current data. Pause here and review the table and experiment components above; what would you predict?
A common response is 10, with the justification that 20% of the beads in the box are red, and the paddle for sampling them has 50 indentations, 20% of 50 = 10. Some more sophisticated suggestions Deming heard included:
Probability
The population will just “average-out” to 10
Mathematical Law of Large Numbers, ie. as a sample size grows, its mean gets closer to the average of the whole population.
Central Limit Theorem, ie. the distribution of sample means approximates a normal distribution as the sample size gets larger.
In response, he’d give a terse: “Wrong.” Why? Because we have no rational basis for making that prediction, ie. they are just opinions unsupported by theory.
You understand what a rational prediction is? It is one that you can describe. It is one that you can explain. Anybody else may agree or disagree with the method. We can predict rationally that if we had another four days work, the results would fall within these limits. We do not know that. If we had the other four days, then we’d know. Empirical evidence is never complete. I keep emphasizing that…
Before we did the experiment, as of this morning, would you have predicted that x-bar would settle down to anything? No! Now that’s not a matter of opinion. I’m not advancing something and asking you to examine it. It is not that kind of thing. The answer is no. You could not and should not, make any such prediction…
Walton, Mary. The Deming Management Method. Perigee Business. (pp. 48-49)
He’d then ask whether anyone had considered the paddle in their predictions, revealing cumulative averages of the paddles he had used for teaching the experiment over four decades:
Paddle No. 1 was made of aluminum in 1942 by a friend at RCA, Camden. I used it in the United States. I taught the Japanese with it. Paddle No. 2 was smaller and easier than No. 1 to carry, made for me by Mr. Bill Boller of Hewlett-Packard. No. 3 was made of apple wood, beautiful, but a bit bulky. No. 4 was made for me of white nylon by AT&T technologies in Reading…
No one could predict what x-BAR will cumulate for any given paddle.
Deming, W. Edwards. The New Economics, 3rd Ed (MIT Press) (pp. 114-115). The MIT Press.
Thus, while probabilities and various statistical theory tells us we should expect the cumulative average to be 10, it is not and we can plainly see it. What is going on, here? Why? As Deming observes in the second excerpt at the top of this post, “Statistical theory (theory of probability) as taught in the books for the theory of sampling and theory of distributions applies in the use of random numbers, but not in experiences of life.”
There is a profound lesson in this “stupidly simple” exercise (as Deming called it): If we run our organizations and businesses using summary statistics to make predictions against a system, we’re asking for trouble because they presume the frame of data they examine is finite and do not consider the variation that emerges from interaction of components in the system. The evidence from these interactions is never complete.
Drawing by Random Numbers
So, under what circumstance could we expect the cumulative average of red beads drawn over time to be 10?
Deming proposed this would only be the case if the lots of beads were selected by random numbers, ie. numbering each bead and consulting a table to individually select them randomly by their index. Unlike mechanically sampling using a physical paddle and beads, with all the attendant variation between the components of the system, the distribution is always uniform: 80/20. Each bead stands as much a chance as any other of being selected. Probability makes sense, here.
We can easily prove this by writing a program to simulate drawing random lots and run it over hundreds of iterations and calculate the cumulative averages. I did just this using a bit of Python code (see source here) and ran ten successive equivalents of 300 Red Bead Experiments generating the following results:
Unsurprisingly, the math works when the system and all of its components are abstracted away. Incidentally, this also demonstrates what is missing from computer-based simulations of the experiment you might run across.
A Rational Basis for Prediction: Statistical Control
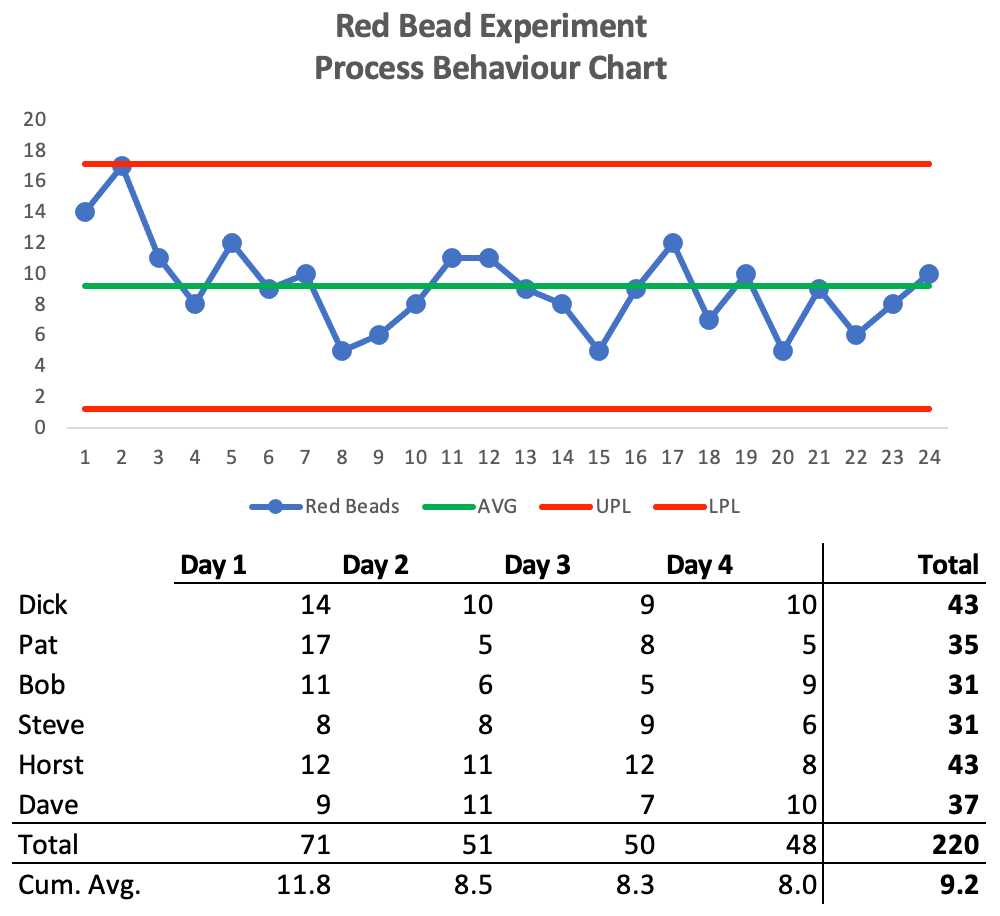
Deming asserts that the only way we can make rational predictions about future performance is to know whether the system is under statistical control. As I wrote in my December 6th newsletter on Tampering, the operational definition of a stable, predictable system is one where all data points representing the system are within the control limits on a Process Behaviour Chart, such as the one shown below based on one of Dr. Deming’s experiment runs listed above:
Dr. Deming’s analysis, using knowledge of variation of a system and statistical control tells him that this system is stable, and predictable. A rational basis for predicting future outcomes:
Nobody exceeded the upper limit. Tried to. Came close. Didn’t make it, though. All the lots, all twenty-four, stayed within the control limits. Pretty good sign that we have a moderately good state of statistical control. I never use the word perfect because there is no such thing… And look at the variation. Constant cause system means stability in the sense that you may compute the limits of variation for the future. All future? No. Let’s say immediate future, on the basis of the twenty-four lots that we have… If we had another forty-eight worth, we could combine them, to compute new limits for the future. It would probably turn out to be just about what we have now.
Walton, Mary. The Deming Management Method. Perigee Business. (pp. 47-48)
Example: Forecasting
So-armed with our knowledge on the divergence between summary statistics and predictions in the real world, let’s turn our attention to the common problem of forecasting delivery in business. Consider the following run-chart showing sample data of a software delivery team’s daily throughput or work items completed per day which I obtained from a site offering statistical analysis tools for predicting delivery of software projects (source):
Question: What is your prediction for what the team will deliver in the future? What is the basis for your prediction?
It’s an unfair question, of course, since you get no knowledge of the hypothetical system, but you may note on the site there’s an array of tools that can statistically slice, dice, and summarize this data to aid in predicting the future - even a Monte Carlo simulation. Summary statistics aside, the first question on our minds should be: Does this data reflect a stable system?
If we extract the data and plot it on a Process Behaviour Chart, as Dr. Deming did with results from the Red Bead experiment we can immediately see multiple signals of potential special causes on both the X-Chart (top) and mR Chart (below). On some days, the team was delivering well in excess of their usual capability - why? Were some work items being banked up for a batched release? Was it the result of management pressure to work longer hours? Did the sizing of work change? Were they quick one-time adjustments?
We can also see that many of the “peaks” are followed by crashes down either just above or below the central line or mean, causing corroborating signals on the mR chart. Are these explainable? In any event, management must investigate each and work on stabilizing the system before making any predictions on future daily throughput.
While this is just sample data, consider it through the lens of the Red Bead Experiment we discussed earlier: a stable system, exhibiting predictable variation according to the interaction of the paddle with the beads in a known distribution that should statistically yield a cumulative average of 10 red beads over time, yet doesn’t. Were the system unstable, perhaps due to swapping paddles or irregularly sized beads, or tampering, consider that the delta between the statistically-predicted cumulative average and reality would be even larger.
In the case of our fictional software team, we are handicapped in not being able to see the interaction of “red beads” or other components in the system, so the actual distributions we would base our predictions upon are that much more ephemeral. The delta between what we think we know, using summary statistics, and reality is an “unknown, unknowable” quantity, but presents a very real conundrum for management who without this knowledge are flying blind. As Dr. Deming once warned: “If you run your business that way, you’ll be in trouble. Really be in trouble.”
Summary
In this post, we’ve learned:
What constitutes a rational basis for prediction and what does not;
How summary statistics can mislead and be quite divergent from reality
How tests of statistical control using a Process Behaviour Chart can provide a means of making rational predictions for the future
Why to be cautious of automated tools that offer multiple statistical analyses of data without first determining if they describe a stable system
Reflection Questions
Consider the quoted excerpts by Dr. Deming in this post and his guidance on what constitutes a rational basis for prediction. Do you agree with Dr. Deming’s debriefing and distinction between mechanical and random sampling with respect to statistical predictions? What automated tools are you relying on to provide statistical summaries and attendant predictions of real-world, physical systems? What is the delta between the statistic and reality? How would you find out? Is the system the statistics summarize in a good state of statistical control? What data could you use to find out?