Example of a simple loss function. A loss function describes the losses that a system suffers from different values of some adjustable parameter. Use of a loss function is restricted to the realm of losses that are measurable.
The most important use of a loss function is to help us change from a world of specifications (meet specifications) to continual reduction of variation about the target, through improvement of processes…
But if we move far out from the minimum [loss around the target], there will be substantial loss. Somebody must pay for this loss — Dr. Taguchi called it a loss to society (September 1960). We all help to pay for a mistake, a breakdown, failure (bankruptcy) of a company, inept management.
- Deming, W. Edwards. The New Economics, 3rd ed. (pp. 149-151)
“We in America have worried about specifications: meet the specifications. In contrast, the Japanese have worried about uniformity, working for less and less variation about the nominal value—e.g., diameter 1 cm.” (Contributed by John Betti, Ford Motor Company.)
This statement is in accord with a formal model introduced by G. Taguchi years ago, which leads to lower and lower costs as quality is improved.
Deming, W. Edwards. Out of the Crisis (MIT Press) (pp. 49-50). The MIT Press. Kindle Edition.
THE AIM of this post is twofold: First, to provide a gentle introduction to Dr. Genichi Taguchi’s revolutionary model for continual quality improvement that became a mainstay of Dr. Deming’s management theory, and second, to demonstrate that the thinking it describes is more aligned with reality and how you think and act as an individual than the common “meets specifications” thinking it opposes.
As legend has it, Dr. Deming first became aware of Dr. Taguchi’s model and thinking while attending a conference in Tokyo in September 1960 where Taguchi presented his seminal paper describing the loss function curve. Even years later, Deming would recall the experience by noting “I was there”, to double-underline the importance of what he learned and why it was so impactful.
However, before going further, we need an operational definition for a loss function:
In mathematical optimization and decision theory, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event.
Source: Wikipedia
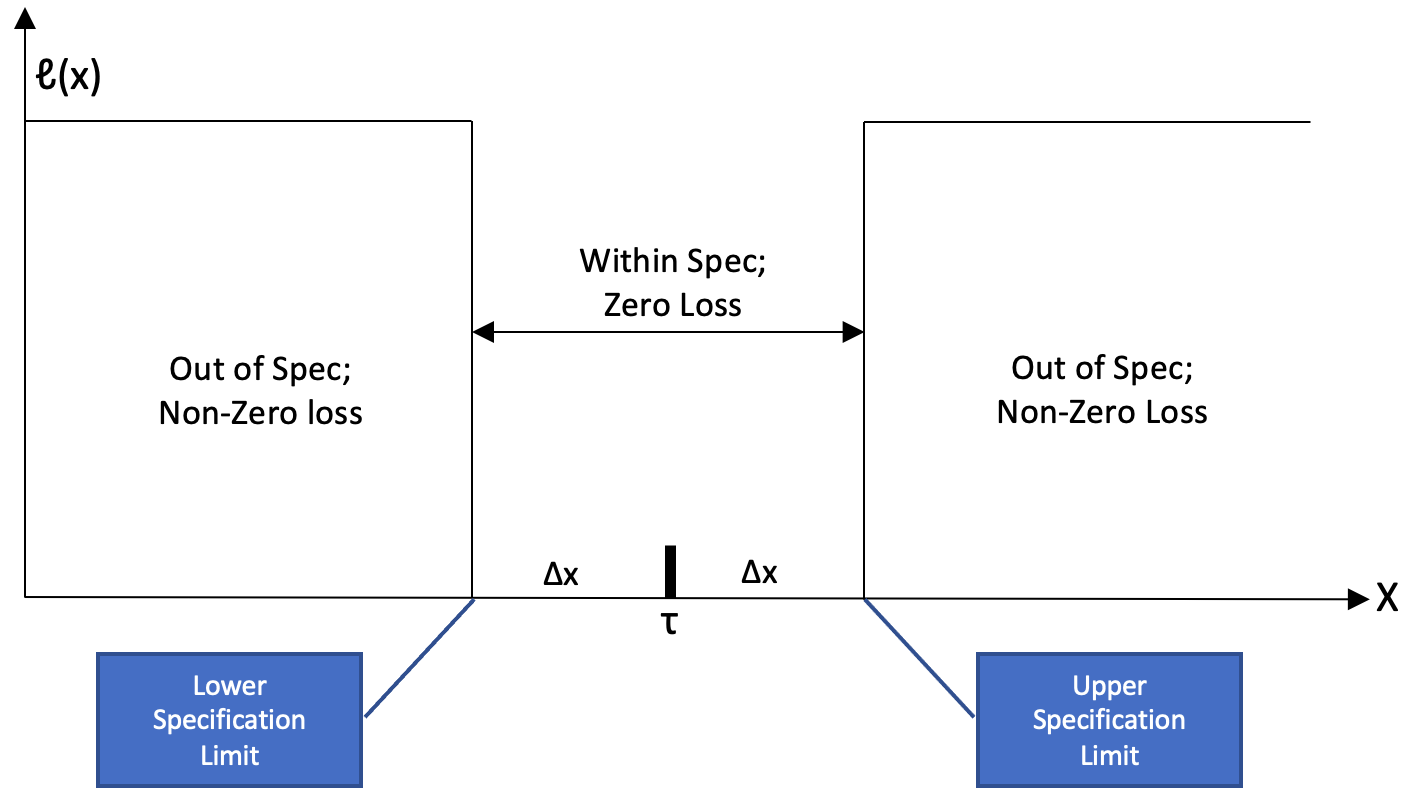
The most common loss function we encounter every day at work or in society comes from arbitrary specification limits or boundaries placed around a target, for which there is a consequence for crossing, ie. a “loss”. These typically take the form of a “step function” as shown below - I’ve based this on a diagram Dr. Don Wheeler and David Chambers use in their text, Understanding Statistical Process Control (p. 142):
In this model, τ represents our ideal target surrounded by specification limits set at Δx, with loss shown on the vertical axis as ℓ(x) and the characteristic value X we’re interested in evaluating on the horizontal axis. As long as X is within the specification limits, ℓ(x) will be zero, otherwise a non-zero loss is incurred. It’s a binary view of the world: Our process either meets the specifications, or does not. How well does this reflect reality?
A troubling weakness of this model emerges as we get close to a specification limit and are asked to rationalize how a result just inside is materially different from one just outside. As Dr. Deming notes in Out of the Crisis, “There is obviously something wrong when a measured characteristic barely inside a specification is declared to be conforming; outside it is declared to be non-conforming.”
We encounter this thinking in our everyday lives wherever we are measured on our conformance to a target. What really is the difference between the lower-end of an A- and the upper end of a B+? If we go 9km/h over the speed limit vs. 10km/h? If a year-end bonus moves us just inside the next tax bracket? The difference in how a school or product is ranked from one category of preference or excellence to another. How we sort recyclables of mixed-materials. How we evaluate a product made of 75% wool.
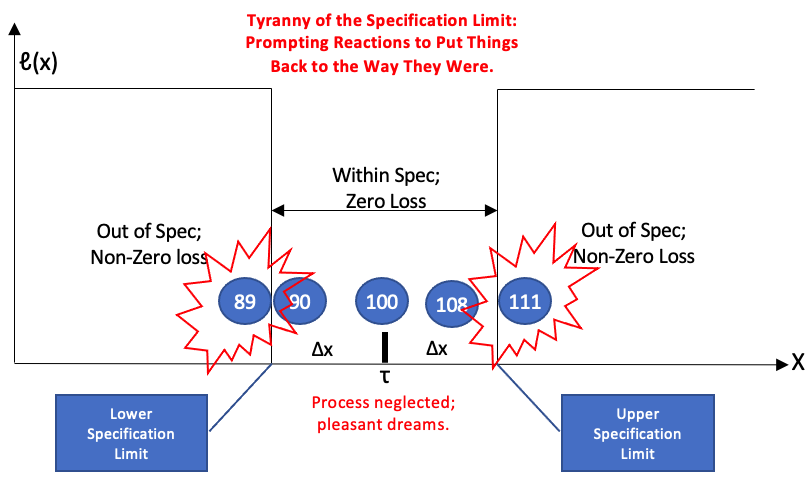
In organizations that are managed by a “meets specifications” mindset, we find the phenomena of the tyranny of the specification limit occurring whenever a process output drifts from “acceptable” to “unacceptable”, as illustrated below. This comes as a consequence of neglecting a process when things appear to be working well and taking action to bring things back in line at the limits. Without knowledge of variation, this invariably makes things worse, as we learned in the Lessons of the Funnel.
Enter: The Taguchi Loss Function
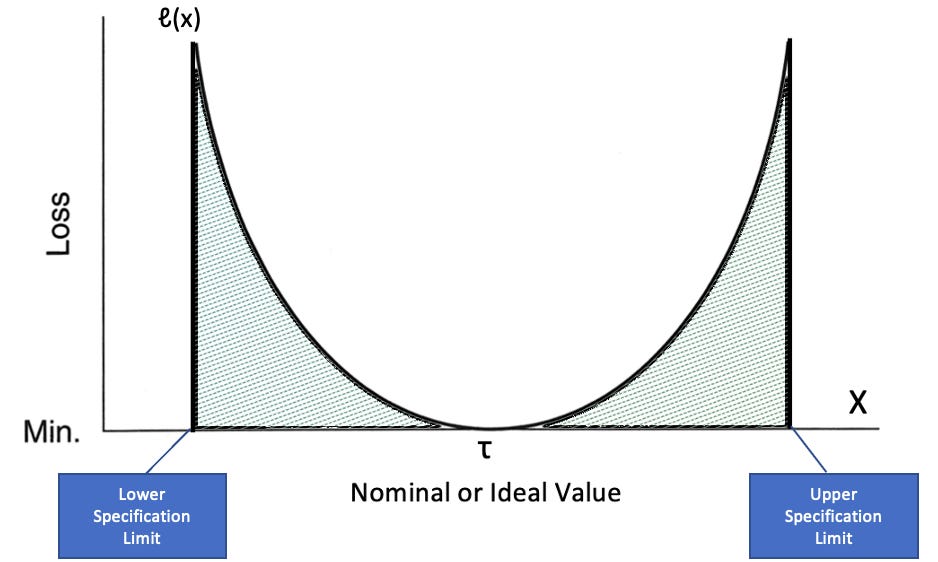
Obviously, we need an antidote to this view of the world that directs our thinking to confusing coincidences and with causes-and-effects and endless arguments about what’s inside or outside a given boundary, one that takes a non-linear systems view of reality into account. This is exactly what Dr. Taguchi proposed with his interpretation of a parabolic loss function, as pictured below. Note, this isn’t the expected form for every loss function: they can assume various shapes and symmetries depending on the application.
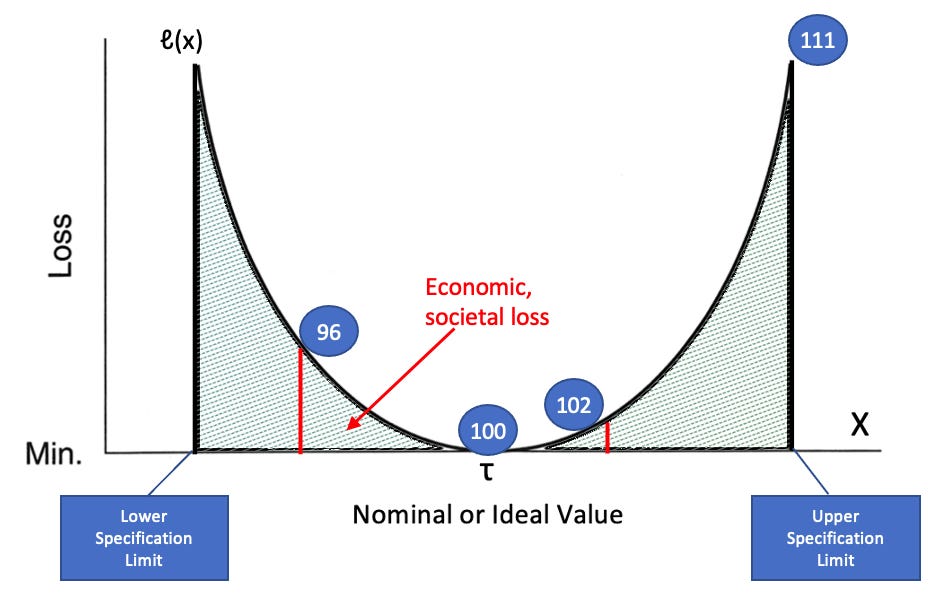
As with the step-function loss curve, we have a target, τ, surrounded by upper and lower specification limits placed along the horizontal axis where we measure the characteristic value, X, of the process. However, instead of a zero-loss channel between the limits, Taguchi (following the lead of mathematicians from as far back as Pierre Simon Laplace) substituted a curve centred on the target where losses, ℓ(x), would be close to zero and increased or decreased in inverse proportion to the distance along the horizontal axis from the target. This is shown as the cumulative shaded area under the curve from the measurement to the target:
Dr. Taguchi, in alignment with Dr. Deming’s view of unknown and unknowable consequences of a satisfied or dissatisfied customer, viewed the losses of failing to mind the variation of a process or product that diverges from its target as not only to the organization but to society. This is a very profound insight, as Dr. Donald Wheeler and David Chambers explain in Understanding Statistical Process Control:
Thus, Dr. Taguchi’s concept of a more realistic Loss Function leads unavoidably to a new definition of world-class quality— “On Target With Minimum Variance.” “On Target” will require that one know the Process Average, and sets the Process Aim in such a way to get the Process Average as close to the Target as possible…
Conformance to Specifications, Zero Defects, Six Sigma Quality, Cost of Quality and all other specification nostrums miss this point. World Class Quality has been defined by “On Target with Minimum Variance” for the past thirty years! The sooner one wakes up to this fact of life, the sooner one can begin to compete.
(p. 146)
Example Application: Choosing a Meeting Duration
While attending the 2018 Deming Institute Annual Conference, I had a conversation with David Langford about how he used the canonical form of the Taguchi Loss Function to help a group of educators determine the ideal length of a status meeting. He plotted intervals on a graph from 5m to 1h and asked the group to vote which were least satisfactory, with zero indicating most satisfaction. After some sorting and discussion, what emerged was a curve centred around 30m, with identified losses for having meetings that either exceeded or fell short of this target:
Reflection Questions
Consider how step-loss functions are used in your organization and by society and the thinking that a “meets specifications” view of the world encourages. What are the consequences to the organization and society when we determine acceptability based on arbitrary limits? What implications are there for improvement of quality? Compare and contrast your observations with the model proposed by Dr. Taguchi. How does his loss function comport with reality? What changes would using a Taguchi view of quality bring to your organization? How could you apply this model?